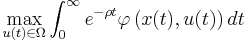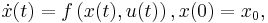DNSS point
DNSS points arise in optimal control problems that exhibit multiple optimal solutions. A DNSS point named alphabetically after Deckert and Nishimura,[1] Sethi,[2][3] and Skiba[4]
named alphabetically after Deckert and Nishimura,[1] Sethi,[2][3] and Skiba[4] is an indifference point in an optimal control problem such that starting from such a point, the problem has more than one different optimal solutions. A good discussion of such points can be found in Grass et al.[5]
is an indifference point in an optimal control problem such that starting from such a point, the problem has more than one different optimal solutions. A good discussion of such points can be found in Grass et al.[5]
Contents |
Definition
Of particular interest here are discounted infinite horizon optimal control problems that are autonomous.[6] These problems can be formulated as
s.t.
where 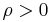 is the discount rate,
is the discount rate, 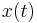 and
and 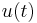 are the state and control variables, respectively, at time
are the state and control variables, respectively, at time  , functions
, functions  and
and  are assumed to be continuously differentiable with respect to their arguments and they do not depend explicitly on time
are assumed to be continuously differentiable with respect to their arguments and they do not depend explicitly on time  , and
, and  is the set of feasible controls and it also is explicitly independent of time
is the set of feasible controls and it also is explicitly independent of time  . Furthermore, it is assumed that the integral converges for any admissible solution
. Furthermore, it is assumed that the integral converges for any admissible solution 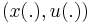 . In such a problem with one-dimensional state variable
. In such a problem with one-dimensional state variable  , the initial state
, the initial state 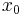 is called a DNSS point if the system starting from it exhibits multiple optimal solutions or equilibria. Thus, at least in the neighborhood of
is called a DNSS point if the system starting from it exhibits multiple optimal solutions or equilibria. Thus, at least in the neighborhood of 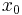 , the system moves to one equilibrium for
, the system moves to one equilibrium for  and to another for
and to another for 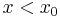 . In this sense,
. In this sense, 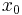 is an indifference point from which the system could move to either of the two equilibria.
is an indifference point from which the system could move to either of the two equilibria.
For two-dimensional optimal control problems, Grass et al.[5] and Zeiler et al.[7] present examples that exhibit DNSS curves.
Some references on the application of DNSS points are Caulkins et al.[8] and Zeiler et al.[9]
History
Suresh P. Sethi identified such indifference points for the first time in 1977.[2] Further, Skiba,[4] Sethi,[3] and Deckert and Nishimura[1] explored these indifference points in economic models. The term DNSS (Deckert, Nishimura, Sethi, Skiba) points, introduced by Grass et al.,[5] recognizes (alphabetically) the contributions of these authors.
These indifference points have been referred to earlier as Skiba points or DNS points in the literature.[5]
Example
A simple problem exhibiting this behavior is given by 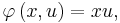
 and
and ![\Omega = \left[-1, 1\right]](/2012-wikipedia_en_all_nopic_01_2012/I/834f3b5ef8fc5e2c53d9f939d984aedb.png) . It is shown in Grass et al.[5] that
. It is shown in Grass et al.[5] that 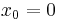 is a DNSS point for this problem because the optimal path
is a DNSS point for this problem because the optimal path 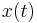 can be either
can be either 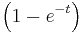 or
or 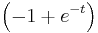 . Note that for
. Note that for 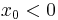 , the optimal path is
, the optimal path is 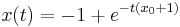 and for
and for 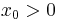 , the optimal path is
, the optimal path is 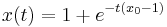 .
.
Extensions
For further details and extensions, the reader is referred to Grass et al.[5]
References
- ^ a b Deckert, D.W.; Nishimura, K. (1983). "A Complete Characterization of Optimal Growth Paths in an Aggregated Model with Nonconcave Production Function". Journal of Economic Theory 31 (2): 332–354. doi:10.1016/0022-0531(83)90081-9.
- ^ a b Sethi, S.P. (1977). "Nearest Feasible Paths in Optimal Control Problems: Theory, Examples, and Counterexamples". Journal of Optimization Theory and Applications 23 (4): 563–579. doi:10.1007/BF00933297.
- ^ a b Sethi, S.P. (1979). "Optimal Advertising Policy with the Contagion Model". Journal of Optimization Theory and Applications 29 (4): 615–627. doi:10.1007/BF00934454.
- ^ a b Skiba, A.K. (1978). "Optimal Growth with a Convex-Concave Production Function". Econometrica 46 (3): 527–539. doi:10.2307/1914229. JSTOR 1914229.
- ^ a b c d e f Grass, D., Caulkins, J.P., Feichtinger, G., Tragler, G., Behrens, D.A. (2008). Optimal Control of Nonlinear Processes: With Applications in Drugs, Corruption, and Terror. Springer. ISBN 978-3-540-77646-8.
- ^ Sethi, S.P. and Thompson, G.L. (2000). Optimal Control Theory: Applications to Management Science and Economics. Second Edition. Springer. ISBN 0387280928 and ISBN 0792386086. Slides are available at http://www.utdallas.edu/~sethi/OPRE7320presentation.html
- ^ Zeiler, I., Caulkins, J., Grass, D., Tragler, G. (2009). Keeping Options Open: An Optimal Control Model with Trajectories that Reach a DNSS Point in Positive Time. SIAM Journal on Control and Optimization, Vol. 48, No. 6, pp. 3698-3707.| doi =10.1137/080719741 |
- ^ Caulkins, J. P.; Feichtinger, G.; Grass, D.; Tragler, G. (2009). "Optimal control of terrorism and global reputation: A case study with novel threshold behavior". Operations Research Letters 37 (6): 387–391. doi:10.1016/j.orl.2009.07.003.
- ^ I. Zeiler, J. P. Caulkins, and G. Tragler. When Two Become One: Optimal Control of Interacting Drug. Working paper, Vienna University of Technology, Vienna, Austria